Fenster schließen

1. Basisberechnung des Zahnradsystems A (Entwurf)

Autor: Thomas Stapelfeldt

Für die Berechnung des Zahnradsystems A wird die vom Autor dieses Berichts programmierte Software "Matrix" verwendet. Mit der aktuellen Version können u. a. folgende Berechnungen durchgeführt werden:

1. Aufbau eines Verzahnungsbaukastens nach vorgegebenen Randbedingungen
2. Zahnradberechnung mit und ohne Verknüpfungen
3. Berechnung sämtlicher Verzahnungsteile (Geometrie und Festigkeit)
4. Verwendung eines Werkzeugsystems
5. Grafische Analysen
6. Auslegung der Welle-Nabe-Verbindungen und damit Berücksichtigung der Motorzuordnung (Betriebsfaktoren!)
7. Schnittstellen zur Übergabe von Daten
8. Ausführliche Dokumentation der Ergebnisse
9. Berechnung der Einsparpotentiale

Aufgrund der Unabhängigkeit von Softwareanbietern können Änderungen im Programmcode beliebig und schnell erfolgen. Das Programm ist unverkäuflich.

Das in diesem Beispiel berechnete Zahnradbasissystem beruht auf 6 Baugrößen 2-stufiger Stirnradgetriebe mit jeweils 12 möglichen Übersetzungen in der motorseitigen Getriebestufe, die dann mit jeweils 2 weiteren Stirnradstufen abtriebsseitig kombiniert werden. Die 6 Basisachsabstände sind geometrisch gestuft (36 mm bis 80 mm). Die Achsabstände der An- und Abtriebsstufen sind bei jeder Baugröße in der Basisversion gleich (kein Achsversatz). Der hier verwendete Ausdruck Basisversion bezieht sich also zunächst auf ein Zahnradsystem, das die einfachen Verknüpfungen der Zahnradberechnungen einhält und zum Ziel hat, möglichst ähnliche Übersetzungreihen für alle Baugrößen zu erzeugen.

Abb. 1: Basiswerte des Zahnradsystems

Mit den Basiswerten nach Abb. 1 wird die erste Version des Zahnradbaukastens berechnet. Die 12 Zielübersetzungen liegen zwischen 1,244 und 12,000 und die Achsabstände sind mit dem Faktor 1,173 gestuft.

Mit definierten Ausgangswerten für die Verzahnungen wie z. B. Schrägungswinkel und Mindestzähnezahl für Ritzel wird eine erste Berechnung durchgeführt (Abb. 2). Die Verzahnungsgeometrie der Ritzel wird in den Diagonalen beibehalten, zu erkennen z. B. an den gelb hinterlegten Kästchen mit den Indizes 6.1 bis 1.6. Prinzipiell wäre dieses Zahnradsystem bereits verwendbar. Durch Änderungen spezifischer Zahnraddaten nach Abb. 3 (z. B. Zähnzahlen, Modulgrößen und Werkzeugdaten) kann das System zunächst weiter optimiert werden. Hauptziele sind beispielsweise die Bildung von Modulgruppen sowie die Einhaltung bestimmter Grenzwerte wie Kopfspiel oder spezifisches Gleiten. Weiterhin können einzelne Radsätze ausgeblendet und damit als nicht verwendet markiert werden. Dies wäre insbesondere bei "ungeordnet" berechneten Systemen sinnvoll, wenn beispielsweise Achsabstände vorgegeben werden oder maximale Raddurchmesser begrenzend sind (z. B. bei SEW). Einzelne oder sämtliche Radsätze können auch "abgekoppelt" werden, wobei dann keine Verknüpfung zu anderen Radsätzen mehr besteht (z. B. bei Abtriebsstufen).

Abb. 2: Ergebnisse der ersten Berechnung der Variationsstufen

Abb. 3: Änderungsmöglichkeiten für jeden Radsatz

Nach der vorläufigen Optimierung ergibt sich ein Zahnradsystem wie in Abb. 4 dargestellt. In der Abbildung ist erkennbar, dass nun 6 Diagonalen die Modulgröße 1,00 mm benutzen und dass das System insgesamt mit lediglich 4 Modulgrößen auskommt. Natürlich sind Kriterien wie beispielsweise Festigkeit und Überdeckung bei der Modulwahl zu berücksichtigen. Für jeden Radsatz zeigt ein Ampelsystem an, ob die Vorgaben und Grenzwerte erfüllt werden. Bis auf einen Radsatz (gelbes Kästchen für ganzzahlige Übersetzung) sind sämtliche Kriterien erfüllt. Die Übersetzungen liegen alle innerhalb der zulässigen Toleranzbereiche (hier +/- 2 %) der Zielübersetzungen.

Abb. 4: ZRS A nach vorläufiger Optimierung mit Modulgruppen

Die weiteren Abbildungen zeigen noch einige Ergebnisdarstellungen und sollen lediglich den Umfang der Software andeuten. Abb. 5 zeigt sämtliche Achsabstände und Übersetzungen in logarithmischer Darstellung. So ist sowohl die gleichmäßige Achsabstandsstufung als auch die der zunehmende Übersetzungsstufensprung hin zu kleinen Übersetzungen erkennbar. Die Darstellung der Stufensprünge für die Übersetzungen im Vergleich zur Vorgabe verdeutlicht den Zusammenhang im Diagramm der Abb. 6. Am Rande sei erwähnt, dass es auch möglich ist, geometrisch gestufte Übersetzungsreihen näherungsweise zu erreichen (siehe ZRS B). Unter anderem kann dies mittels Aufteilung des Systems geschehen, beispielsweise Gruppen von 8 und 4 Übersetzungen.

Abb. 5: Logarithmische Darstellung von Übersetzungen und Achsabständen

Abb. 6: Übersetzungsstufensprünge der Baugrößen

Abb. 7: Grafik eines einzelnen Radsatzes

Abb. 8: Grafische Gesamtübersicht sämtlicher Radsätze

Die einzelnen Verzahnungen können nun (auch mit den gewählten Werkzeugen) grafisch begutachtet werden (Abb. 7). Eine Gesamtübersicht der Zahnprofile (Abb. 8) kann Hinweise auf Ungereimtheiten aufzeigen. Die Verzahnungssicherheiten können näherungsweise berechnet werden, wobei aufgrund der komplexen Bedingungen (Motorwellen oder Kupplungen mit Lagern usw.) hier keine exakten Berechnungen erfolgen können. Die Erfahrung hat jedoch gezeigt, dass mit entsprechenden Annahmen aussagefähige Ergebnisse erreichbar sind. Die Ergebnisse in Abb. 9 zeigen zudem auch Warnungen bei Unterschreitung der vorgegebenen Mindestsicherheiten an.

Abb. 9: Verzahnungssicherheiten

Um das mögliche Einsparpotential bei den Verzahnungsteilen zu ermitteln müssen die Welle-Nabe-Verbindungen (WNV) berücksichtigt werden. Aufgrund der Zusammenhänge von Gesamtübersetzungen, zulässigen Getriebelasten (auch durch Wälzlager) und Betriebsfaktoren ist es erforderlich, dass die antreibenden Ritzel unterschiedliche Abmessungen bei den WNV besitzen. Das Programm kann die Ritzel entweder mit Bohrung und Passfeder oder als Schaftritzel ausführen, also Formschluss oder Kraftschluss (Abb. 10). Natürlich sind auch Kombinationen denkbar, beispielsweise Presssitz und Kerbverzahnung. Entscheidend ist hier einerseits die Vorgabe durch den Motor (bei Direktanbau) und andererseits die Machbarkeit aufgrund der Übersetzungen (Durchmesser). Zur Bestimmung der Ritzel-Gesamtzahl kann das Programm eine Motorbaureihe mit entsprechenden Vorgaben benutzen und diese dann für einen Betriebsfaktorbereich zuordnen.

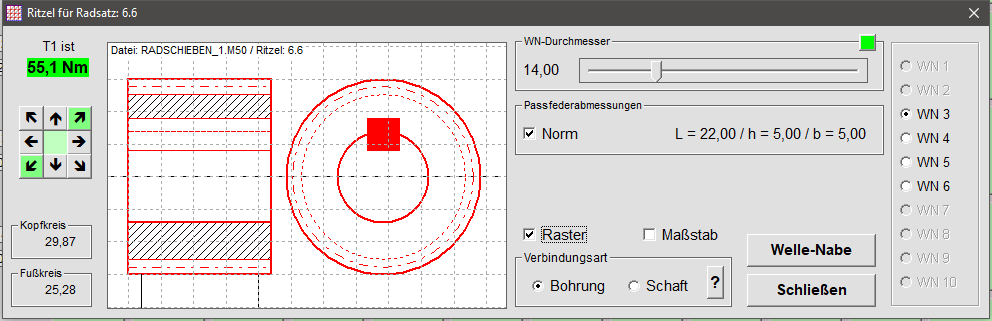
Abb. 10: Welle-Nabe-Verbindung für Ritzel

Eine endgültige Zuordnung von Getrieben und Motoren sollte mit einem separaten Programm erfolgen da hier noch weitere Faktoren (z. B. Wirkungsgrad und Dynamik) in die Berechnungen einfließen. Mit dem Programm "Matrix" ist das Einsparpotential näherungsweise bestimmbar indem sämtliche Ritzelvarianten aufsummiert werden. Bei der hier berechneten Baureihe werden etwa 56 Ritzel benötigt (siehe unten rechts in Abb. 11).

Abb. 11: Gesamtzahl der Ritzel

Mit einem herkömmlichen System, also ohne Wiederverwendung, wären etwa 175 Ritzel für den direkten Motoranbau notwendig. Das "Durchschieben" und damit die Wiederverwendung der Ritzel reduziert deren Anzahl also um etwa 68%.

Falls die Motorkonstruktionen bereits bekannt sind, bietet das Programm die Möglichkeit zumindest einen näherungsweisen Eindruck von der Motor-Getriebe-Kombinatorik zu bekommen. Motorendateien mit auf wesentliche Daten reduziertem Inhalt können editiert und dann für die Berechnung der notwendigen Ritzel benutzt werden. Wird beispielsweise die Motorbaureihe nach Abb. 12 auf den berechneten Zahnradbaukasten in einem definierten Betriebsfaktorbereich angewendet, dann werden die Schaftdurchmesser nach Abb. 13 zugeordnet und die Gesamtzahl der notwendigen Ritzel beläuft sich auf 172.

Abb. 12: Editieren einer Motorendatei

Abb. 13: Zuordnung der Motoren und Ritzelschaftdurchmesser

Die abschließende Berechnung bezieht sich auf die Übersetzungskombinatorik für 2- bis 4-stufige Getriebe. Abb. 14 zeigt die Variationsstufe in Kombination mit 2 Abtriebsstufen für die Baugröße G 302. Auch hier gibt die logarithmische Darstellung Auskunft über die Gleichmäßigkeit der Stufensprünge.

Abb. 14: Gesamtübersetzungen einer 2-stufigen Getriebebaugröße

Abb. 15a: Anzahl und Losgrößen der Ritzel

Abb. 15b: Beispieldarstellung für sämtliche Ritzelausführungen

Wenn die genauen Verkaufszahlen und damit die Losgrößen der Verzahnungsteile bekannt sind, so lassen sich die Ergebnisse qualitativ wie in Abb. 15a darstellen. Das Diagramm zeigt auf der Abszisse die Anzahl der Ritzelvarianten und auf der Ordinate die jeweiligen Losgrößen. Die Anzahl der Varianten wird deutlich reduziert und die Losgrößen werden deutlich gesteigert (oben das alte, unten das neue System) wobei die Summe der Stückzahl insgesamt beibehalten wird. Mit ähnlichen Einsparergebnissen sind bisher zahlreiche Zahnradbaukästen neu berechnet und produziert sowie unzählige Varianten analysiert worden. Konstruktiv lassen sich die Ritzel leicht in einer Übersicht prüfen (Abb. 15b).

Zum Seitenanfang