2. Zahnradsystem B mit geometrisch gestuften Übersetzungsreihen (Entwurf)
Autor: Thomas Stapelfeldt
Die Hauptziele dieser Berechnungen sind möglichst gleichmäßige Übersetzungsstufensprünge und die hohe Ausnutzung der Übersetzungen; es sollte also möglichst zu keinen Überschneidungen bei den Werten der Gesamtübersetzungen kommen. Die Einhaltung der "Zielübersetzungen" ist keine strenge Bedingung, sodass es zu "Verschiebungen" der Übersetzungsbänder kommen kann.
In Abb. 16 werden die Ergebnisse der einzelnen Übersetzungsstufensprünge des ZRS A violett dargestellt. Die 11 Stufensprünge der 12 Zielübersetzungen sind ungleichmäßig und wachsen zu den kleinen Übersetzungen hin an (siehe auch Abb. 6).

Abb. 16: Basis ZRS A mit den Übersetzungsstufensprüngen
Abb. 17 zeigt die Abweichungen der Stufensprünge von ZRS A zu der Vorgabe von φ=1,225. Das primäre Ziel für ZRS C besteht in der Einhaltung möglichst konstanter Übersetzungsstufensprünge. Ein möglichst konstanter Stufensprung würde quasi an die Gesamtübersetzung durchgereicht. Es geht also in erster Linie nicht um die Einhaltung der Übersetzungswerte.

Abb. 17: ZRS A und Stufensprungabweichung
Wie könnte also ein Zahnradsystem der Variationsstufe mit möglichst konstanten Übersetzungsstufensprüngen aussehen? Im ersten Schritt werden für eine Baugröße (hier G 402) die Übersetzungen berechnet (Abb. 18); mit dem Ergebnis, dass die höchste Übersetzungsabweichung bei ca. 1,2% liegt. Der Stufensprung dieser Baugröße ist dann nahezu konstant (Abb. 19).

Abb. 18: Zwischenergebnis für das ZRS B

Abb. 19: Berechnete Stufensprünge für Baugröße G 402 im 1. Berechnungsschritt
Ausgehend von der Berechnung für G 402 sind sämtliche Radsätze dahingehend modifiziert worden, dass die Abweichungen für φ möglichst innerhalb einer zulässigen Fehlerbandbreite von 1,225 +/- 3% liegen (1.188...1,262). Das Ergebnis in Abb. 20 zeigt, dass lediglich 2 Radsätze (rot gerahmt) diese Bedingung knapp nicht erfüllen.

Abb. 20: Berechnete Stufensprünge für ZRS B im Toleranzbereich 3%
Die in Abb. 20 orange gefärbten Radsätze sind vom System entkoppelt und separat berechnet worden. Die Ritzel werden hier also nicht diagonal wieder benutzt und die Gesamtteilezahl erhöht sich leicht gegenüber der von ZRS A. In Abb. 21 ist eine relativ gleichmäßige Verteilung der Übersetzungen für jede Baugröße erkennbar, was sich letztendlich auch im Stufensprung-Diagramm widerspiegelt (Abb. 22).

Abb. 21: Verteilung der Übersetzungen für ZRS B
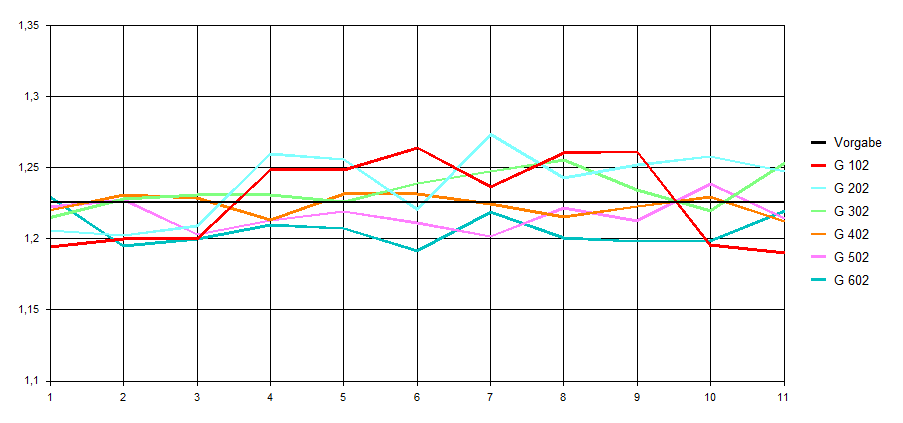
Abb. 22: Verlauf der Stufensprünge für ZRS B

Abb. 23: Gesamtübersetzungen der 2-stufigen Getriebegrößen für ZRS B
Die 6 Diagramme in Abb. 23 zeigen auch die relativ gleichmäßigen Abstufungen bei den Gesamtübersetzungen. Zudem kommt es zu keinen Überschneidungen der Übersetzungswerte, sodass die möglichen Radsatzkombinationen zu 100% genutzt werden. Natürlich könnten die Gesamtübersetzungsbänder noch verschoben werden um Minimal- und Maximalwerte anzugleichen.
Zum Seitenanfang